World Affairs: Integration By Parts Examples

FORMULA FOR INTEGRATION BY PARTS:

Now Here are few examples for you. If You Have any confusion regarding them you can comment below. So I will help you out. Thanks

Example No. 1
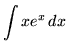Integrate $\displaystyle{ \int {x e^x} \,dx }$ .
Solution:-

Let

$u = x \ \$ and $\ \ dv = e^x dx$

So That

$du = (1) dx = dx \ \$ and $\ \ v = e^x$ .

Therefore:

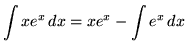
$\displaystyle{ \int { x e^x } \,dx } = \displaystyle{ x e^x - \int { e^x} \,dx }$

$= \displaystyle{ x e^x - e^x + C }$ .

Example No. 2
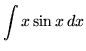Integrate $\displaystyle{ \int { x \sin {x}} \,dx }$ .
Solution:

Let

$u = x \ \$ and $\ \ dv = \sin {x} \ dx$

so that

$du = (1) dx = dx \ \$ and $\ \ v = -\cos{x}$ .

Therefore,

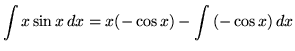
$\displaystyle{ \int { x \sin {x}} \,dx } = \displaystyle{ x (-\cos{x}) - \int { (-\cos{x}) } \,dx }$

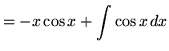
$= \displaystyle{ -x \cos{x} + \int { \cos{x} } \,dx }$

$= -x \cos {x} + \sin{x} + C$ .

Example No. 3

Integrate 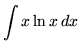$\displaystyle{ \int {x \ln{x}} \,dx }$ .

Solution:

Let

$u = \ln{x} \ \$ and $\ \ dv = x \ dx$

so that

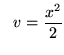$du = \displaystyle{1\over x} \ dx \ \$ and $\ \ v = \displaystyle{x^2 \over 2}$ .

Therefore,

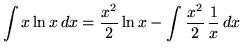
$\displaystyle{ \int {x \ln{x}} \,dx } = \displaystyle{ {x^2 \over 2} \ln{x} - \int { {x^2 \over 2} \, {1\over x} } \,dx }$

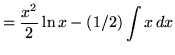
$= \displaystyle{ {x^2 \over 2} \ln{x} - (1/2) \int x \,dx }$

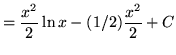
$= \displaystyle{ {x^2\over 2} \ln{x} - (1/2) { x^2 \over 2 } + C}$

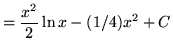$= \displaystyle{ {x^2\over 2} \ln{x} - (1/4) x^2 + C}$ .

Example No. 4

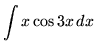
Integrate $\displaystyle{ \int { x \cos {3x} } \,dx }$

Solution:

Let

$u = x \ \$ and $\ \ dv = \cos{3x} \ dx$

so that

$du = (1) dx = dx \ \$ and $\ \ v = (1/3) \sin{3x}$ .

Therefore,

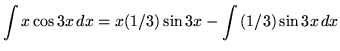
$\displaystyle{ \int { x \cos{3x} } \,dx } = \displaystyle{ x (1/3) \sin{3x} - \int { (1/3) \sin{3x} } \, dx }$

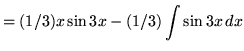
$= \displaystyle{(1/3)x \sin{3x} - (1/3) \int { \sin{3x} } \, dx }$

$= \displaystyle{ (1/3) x \sin{3x} - (1/3) { -\cos {3x} \over 3 } + C }$

$=\displaystyle{ (1/3) x \sin{3x} + (1/9) \cos {3x} + C }$ .

Example No. 5

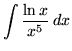
Integrate $\displaystyle{ \int { \ln {x} \over x^5 } \,dx }$
Solution:

Let
$u = \ln x \ \$ and $\ \ dv = \displaystyle{ 1 \over x^5 } \ dx = x^{-5} \ dx$
so that

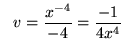$du = \displaystyle{1\over x} \ dx \ \$ and $\ \ v = \displaystyle{ x^{-4} \over -4} = \displaystyle{ -1 \over 4x^4 }$ .

Therefore,

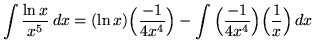
$\displaystyle{ \int {\ln {x} \over x^5 } \,dx } = \displaystyle{ (\ln{x})\Big(... ...ver 4x^4}\Big) - \int {\Big({-1 \over 4x^4}\Big)\Big({1 \over x}\Big) } \, dx}$

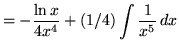
$= \displaystyle{ -{\ln{x} \over 4x^4} + (1/4)\int { 1 \over x^5 } \, dx }$

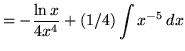
$= \displaystyle{ -{\ln{x} \over 4x^4} + (1/4)\int { x^{-5} } \, dx }$

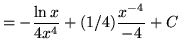
$= \displaystyle{-{\ln{x} \over 4x^4} + (1/4){ x^{-4} \over -4 } + C }$

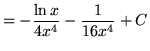$= \displaystyle{-{\ln{x} \over 4x^4} - { 1 \over 16x^4} + C }$ .

Example No. 6

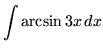
Integrate $\displaystyle{ \int \arcsin 3x \,dx }$
Solution:

Let

$u = \arcsin 3x \ \$ and $\ \ dv = dx = (1) dx$

so that (Don't forget to use the chain rule when differentiating $\arcsin 3x$ .)

$du = \displaystyle{ 1 \over \sqrt{ 1 - (3x)^2 } } (3) dx = \displaystyle{ 3 \over \sqrt{ 1 - 9x^2 } } dx \ \$ and $\ \ v = x$ .

Therefore,

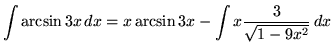
$\displaystyle{ \int \arcsin 3x \, dx } = x \arcsin 3x - \displaystyle{ \int x { 3 \over \sqrt{ 1 - 9x^2 } } \, dx }$

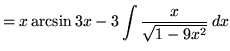$= x \arcsin 3x - \displaystyle{ 3 \int {x \over \sqrt{ 1 - 9x^2 } } \, dx }$ .

Now use u-substitution. Let

$u = 1 - 9x^2$

so that

$du = -18x \ dx$ ,

$(-1/18) du = x \ dx$ .

Then

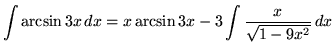
$\displaystyle{ \int \arcsin 3x \, dx } = x \arcsin 3x - \displaystyle{ 3\int {x \over \sqrt{ 1 - 9x^2 } } \, dx }$

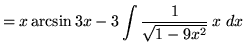
$= x \arcsin 3x - \displaystyle{ 3\int {1 \over \sqrt{ 1 - 9x^2 } } \, x \ dx }$

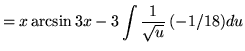
$= x \arcsin 3x - \displaystyle{ 3\int {1 \over \sqrt{ u }} \, (-1/18) du }$

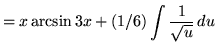
$= x \arcsin 3x + \displaystyle{ (1/6) \int {1 \over \sqrt{ u }} \, du }$

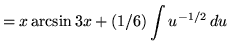
$= x \arcsin 3x + \displaystyle{ (1/6) \int u^{-1/2} \, du }$

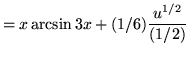$= x \arcsin 3x + (1/6) \displaystyle{ { u^{1/2} \over (1/2) } }$ + C

$= x \arcsin 3x + (1/3) \displaystyle{ (1-9x^2)^{1/2} }$ + C

$= x \arcsin 3x + (1/3) \sqrt{ 1-9x^2 }$ + C .

Example No. 7

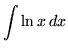Integrate $\displaystyle{ \int {\ln x } \,dx }$ .
Solution:

Let

$u = \ln x \ \$ and $\ \ dv = dx = (1) dx$

so that

$du = \displaystyle{1\over x} \ dx \ \$ and $\ \ v = x$ .

Therefore,

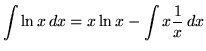
$\displaystyle{ \int { \ln x } \,dx } = \displaystyle{ x \ln{x} - \int {x {1 \over x}} \,dx }$

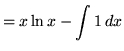
$= \displaystyle{x \ln{x} - \int { 1 } \,dx }$

$= \displaystyle{ x \ln {x} - x + C }$ .

Example No. 8

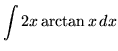
Integrate $\displaystyle{ \int 2x \arctan x \,dx }$
Solution:

Let

$u = \arctan x \ \$ and $\ \ dv = 2x \ dx$

so that

$du = \displaystyle{ 1 \over 1 + x^2 } \ dx \ \$ and $\ \ v = x^2$ .

Therefore,

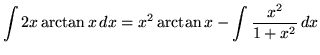
$\displaystyle{ \int 2x \arctan x \, dx } = x^2 \arctan x - \displaystyle{ \int { x^2 \over 1 + x^2 } \, dx }$

(Add $\ 0 = 1 - 1 \$ in the numerator. This will replicate the denominator and allow us to split the function into two parts.)

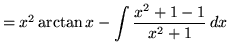
$= x^2 \arctan x - \displaystyle{ \int { x^2 + 1 - 1 \over x^2 + 1} \, dx }$

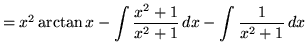
$= x^2 \arctan x - \displaystyle{ \int { x^2 + 1 \over x^2 + 1 } \, dx - \int { 1 \over x^2 + 1 } \, dx }$

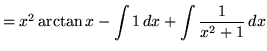
$= x^2 \arctan x - \displaystyle{ \int 1 \, dx + \int { 1 \over x^2 + 1} \, dx}$

$= x^2 \arctan x - x + \arctan x + C$ .

Example No. 9

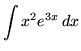
Integrate $\displaystyle{ \int { x^2 e^{3x} } \,dx }$
Solution:

Let

$u = x^2 \ \$ and $\ \ dv = e^{3x} dx$

so that

$du = 2x \ dx \ \$ and $\ \ v = (1/3) e^{3x}$ .

Therefore,

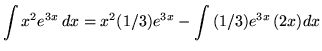
$\displaystyle{ \int { x^2 e^{3x} } \,dx } = \displaystyle{ x^2 (1/3) e^{3x} - \int { (1/3)e^{3x} } \, (2x) dx }$

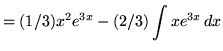$= \displaystyle{(1/3) x^2 e^{3x} - (2/3)\int { x e^{3x} } \, dx }$ .

Integrate by parts again. Let

$u = x \ \$ and $\ \ dv = e^{3x} dx$

so that

$du = (1) dx = dx \ \$ and $\ \ v = (1/3) e^{3x}$ .

Hence,

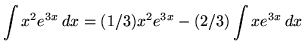
$\displaystyle{ \int { x^2 e^{3x} } \,dx } = \displaystyle{ (1/3) x^2 e^{3x} - (2/3)\int { x e^{3x} } \, dx }$

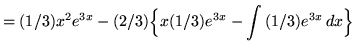
$= \displaystyle{ (1/3) x^2 e^{3x} - (2/3)\Big\{ x (1/3) e^{3x} -\int { (1/3) e^{3x} } \, dx }\Big\}$

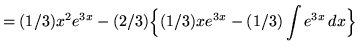
$= \displaystyle{ (1/3) x^2 e^{3x} - (2/3)\Big\{ (1/3)x e^{3x} - (1/3) \int { e^{3x} } \, dx }\Big\}$

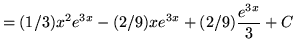
$= \displaystyle{ (1/3){x^2 e^{3x} } - (2/9) xe^{3x} + (2/9) {e^{3x} \over 3 } + C }$

$= (1/3){x^2 e^{3x} } - (2/9) xe^{3x} + (2/27) e^{3x} + C$ .

World Affairs

Translate

Tuesday 11 October 2016

Integration By Parts Examples

No comments:

Post a Comment